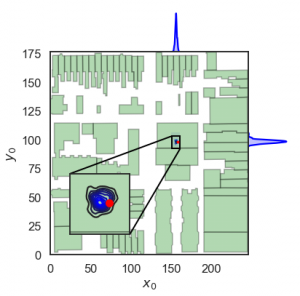
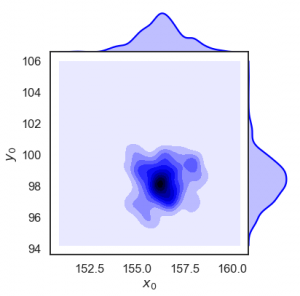
Radiation Source Localization:
The precise and efficient location of mis-appropriated special nuclear material (SNM) is vital to national security. Due to population density, radiological threats to urban areas are particularly dire. Modeling the photon transport phenomena requires many assumptions, and developing a computationally efficient procedure is non-trivial. This research involves surrogate model construction, parameter subset selection, Bayesian model calibration, and uncertainty quantification.
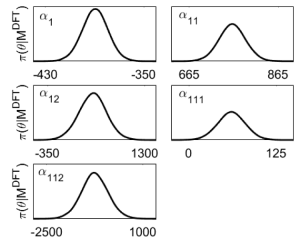
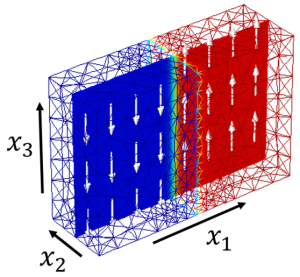
Quantum-Informed Continuum Modeling of Ferroelectric Materials:
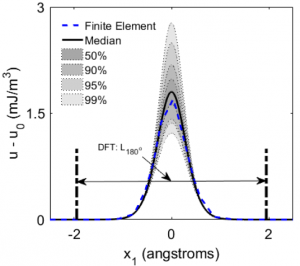
Modeling domain structure evolution at the atomic and electronic scale remains a significant challenge in many active materials (e.g., ferroelectric, ferromagnetic, shape memory alloys). Quantum information from Density Functional Theory (DFT) calculations can be used to better inform a phase-field continuum approximation. Sensitivity analysis is used to determine significant parameters in the continuum approximation, and Bayesian model calibration is used to identify uncertain parameters. The calibration is performed using information from DFT calculations for energy, stress, and polarization at various atomic states.
Relevant Publications:
- Leon, L. S., Smith, R. C., Oates, W. S., Miles, P. R. (2018). Analysis of a Multi-Axial Quantum Informed Ferroelectric Continuum Model: Part 2—Sensitivity Analysis. Journal of Intelligent Material Systems and Structures, 29(13), 2840-2860. https://doi.org/10.1177/1045389X18781024
- Miles, P. R., Leon, L. S., Smith, R. C., Oates, W. S. (2018). Analysis of a Multi-Axial Quantum Informed Ferroelectric Continuum Model: Part 1—Uncertainty Quantification. Journal of Intelligent Material Systems and Structures, 29(13), 2823-2839. https://doi.org/10.1177/1045389X18781023
Fractional-Order Viscoelastic Modeling:
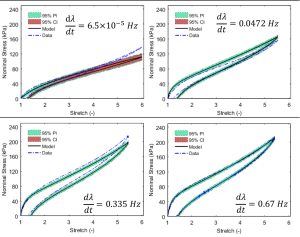
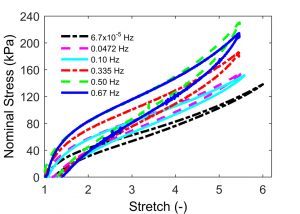
A fractional-order approach to viscoelastic modeling yields parameters that provide better predictions across a broad range of deformation rates. The fractional order represents a scaling on the deformation rate, which is believed to be material dependent. Additional research is focused on improving numerical procedures for fractional-order operators.
Relevant Publications:
- Mashayekhi, S., Miles, P. R., Hussaini, M. Y., Oates, W. S. (2018). Fractional Viscoelasticity in Fractal and Non-Fractal Media: Theory, Experimental Validation, and Uncertainty Analysis. Journal of the Mechanics and Physics of Solids,111, 134-156. https://doi.org/10.1016/j.jmps.2017.10.013
- Miles, P. R., Hays, M., Smith, R. C., Oates, W. S. (2015). Bayesian Uncertainty Analysis of Finite Deformation Viscoelasticity.” Mechanics of Materials, 91, 35-49. https://doi.org/10.1016/j.mechmat.2015.07.002